Решение уравнений, систем и неравенств
Mathematica включает в себя средства поиска корней различных типов уравнений и систем. Чаще всего для этих целей используется функция Solve[eqn, var], где eqn - уравнение или система, задаваемая списком уравнений, var - переменная или список переменных, которые требуется определить. Результат вычислений - список корней (возможно пустой).
Палитра Basic Calculations в разделе Algebra содержит несколько шаблонов для ввода функции Solve (пункт Solving Equations). Обратите внимание, что левая и правые части уравнения соединяются символами ==, например,
Solve[3 x + 9 == 0, x] Solve[x^2 + 2b*x + c == 0, x] Solve[x^2 + 1 == 0, x] Solve[{x==1+2a*y, y==9+2x}, {x,y}]
Решения ищутся на множестве комплексных чисел, причем мнимая единица обозначается символом I. Для тригонометрических уравнений выдается только одно из бесконечного множества решений.
Программа позволяет также решать логарифмические и показательные уравнения. Натуральные логарифмы задаются функцией Log, а логарифмы по произвольному основанию n - в виде Log[n, expr], где expr - аргумент логарифмической функции, например, Log[2, 1024]. Для Эйлеровой константы (основания натурального логарифма) используется обозначение E.
Пример
Следующий фрагмент демонстрирует решение уравнения
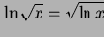
In[12]:= Solve[Log[Sqrt[x]]==Sqrt[Log[x]], x] Out[12]= {{x -> 1}, {x -> E^4}}
Для решения неравенств предварительно следует подключить дополнительный модуль расширения Algebra:
<<Algebra`InequalitySolve`
Имя функции, решающей неравенства, совпадает с названием подпакета - InequalitySolve. Для задания неравенств используют знаки > (строго больше), >= (больше или равно), < (строго меньше) и <= (меньше или равно), например,
In[13]:= InequalitySolve[x^2-1<0,x] Out[13]= -1<x<1
In[14]:= InequalitySolve[x^2/(x^2-1)>=0,x] Out[14]= x<-1 || x==0 || x>1
In[15]:= InequalitySolve[(2x-1)/(4(x+1))<Cos[5Pi/3],x] Out[15]= x<-1
При решении неравенств, отличных от дробно-рациональных, система выдает предупреждение о возможном некорректном решении:
In[16]:= InequalitySolve[2^(x^2)>16,x] InequalitySolve::"npi": " A nonpolynomial equation or inequality encountered. The solution set may be incorrect." Out[16]= x<-2 || x>2
В тех случаях, когда невозможно решить заданное уравнение аналитически, можно приближенно вычислить значение корня следующим образом. Сначала при помощи функции Plot строятся графики левой и правой частей уравнения и по рисунку находится первое приближение x0. Затем для уточнения значения корня применяется функция FindRoot. Если L(x) и R(x) - соответственно левая и правая части уравнения, x - искомый корень, а x0 - его приближенное значение, определенное с помощью графика, то функция для поиска корня имеет вид:
FindRoot[L(x)==R(x), {x,x0}]
Пример
Найдем приближенное решение уравнения ex=x2. Построим графики функций ex и x2, выполнив команду Plot[{Exp[x], x^2}, {x, -1, 1}].
Мы получим изображение графиков функций ex и x2 на одном чертеже для значений аргумента x, изменяющегося на отрезке [-1,1].
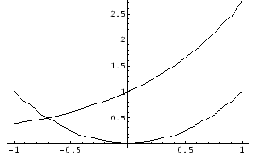
Глядя на графики, видим, что в качестве начального приближения может быть взято значение x0 = -0.5.
Для уточнения решения нашего уравнения воспользуемся командой FindRoot[Exp[x]==x^2, {x, -0.5}] и получим приближенное значение корня x = -0.703467. Если требуется большая точность (но не более 16 знаков после запятой), то можно воспользоваться функцией N. Так, выполнив команду N[FindRoot[Exp[x]==x^2, {x, -0.5}], 16], мы получим приближенное значение корня с точностью до 16 знаков после запятой: x = -0.7034674295409824.
Пример
Как правило, тригонометрические уравнения имеют бесконечно много решений, поэтому можно указывать различные начальные приближения и получать приближенные значения разных корней уравнения. Так, выполнив команду FindRoot[Sin[x^2]==0, {x, 2}], найдем x = 1.77245, а изменив начальное приближение с 2.0 на 3.0, с помощью команды FindRoot[Sin[x^2]==0, {x, 3}] получим приближенное значение другого корня уравнения, а именно x=3.06998.
Задания
- Решите системы уравнений:
1. 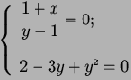
2. 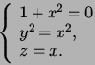
- Решите неравенства:
1. 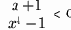
2. 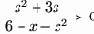
- Найдите приближенно наименьший положительный корень уравнения 1/x2=5 cos x.
- Найдите с точностью 12 знаков после запятой все корни уравнения (1 - x)/(x4 + 1) = sin x, принадлежащие отрезку [-1,4].
